Bundled stories for numerate minds
No method of truth-seeking is immune and no claim to truth is trivial
I grew up fairly exposed to statistics in school. As the level of my exposure increased, the early fascination left its place to growing suspicion. I’ve seen people using statistics to seek truth, but more than everything, I’ve seen people using statistics, independent of the truth-seeking, to support their case, get published and cited, and sometimes simply to appear smart. This didn’t always require a compromise on integrity. At the end of the day, we are often the first believers in our own lies.
We are not critical enough of things that claim to be scientific. We take the words of an average social science professor for granted while we are critical of taxi drivers or handymen. My own experience is that the former group tells more lies. At the end of the day, suits, titles, and jargon are the best covers for nonsense.
Statistics let us analyze multiple observations jointly to come up with general information on the nature of the population at hand. However, grouping anecdotes doesn’t necessarily make them more credible. As Susan Fiske says, “The plural of anecdote is not data, and the plural of opinion is not facts.” You need mathematical rigor and intellectual honesty to claim credibility in statistical analysis.
Statistical models aren’t default-true and we are fools for believing in black-box statistics. They are instead approximations of reality and inaccurate unless proven otherwise. Statistics isn’t magic, it’s just bundled stories for numerate minds.
So far, it sounds like a quite skeptical article and I assure you the rest is consistent with this tone. However, it’s a skepticism coming from an optimistic place—I’m skeptical of the use of statistics by many, yet very much optimistic about its potential in good hands.
In fact, last week I met another investor who has a very inspiring take on data-driven venture investing. The data quality in private markets, including venture capital, has significantly improved over the last decade, and there are immense gains in answering seemingly simple but fundamental questions with high-quality data. So, let’s not forget there are many reasons to be optimistic and for every hundred investors who butcher statistics, there’s an investor who creates miracles out of it.
Before I forget, most of the limitations I describe below also apply to simple qualitative evaluations and pattern matching. So, no method is immune and no claim to truth is trivial.
Answering questions we don’t understand
In his classic book ‘How to Solve It’, George Pólya says, “It’s foolish to answer a question you don’t understand. It is sad to work for an outcome you don’t desire.”
My experience was, for statistical problems, people who lack an understanding of statistics beyond surface-level start from methods rather than questions and have black-box statistical thinking coupled with blind faith in methods. They are the ones who build a very complex machine-learning model to forecast key parameters but cannot share anything about the nature of the problem at hand.
On the contrary, people with a deep understanding of statistics start from the nature of the problem itself and even question the need for using statistical models. They are critical of methods and very thrifty in their use of them. They are the ones who start by making sure that data is high quality and that they understand the basic statistical properties of the problem at hand.
The simplest question of all
Take the very simple question ‘What is the expected return for a venture capital fund?’. Here, a statistician would call venture capital funds population and the answer we’re looking for (the expected return) population mean.
Mean is usually the first question to get answered in any statistical analysis before you find out more about the nature of the population, i.e. other moments like variance and skewness. You can then move on to build statistical models of reality to better understand the causes behind the variance we observe in population parameters. You can even extrapolate your approximation of reality by forecasting these parameters for future observations from the population.
So, it’s not a trivial jump from obtaining data on venture capital funds to using this data to forecast the expected return for a 2015 vintage $80m fund that is based in the US and investing in enterprise software. Before anything, by attempting the answer this question, one inherently assumes that one knows the mean return for a venture capital fund. But, do we know the answer to this simplest question?
Given that it’s not practical to look for all venture investors all around the world and that you might have to dig a considerable number of graves, we use shortcuts to answer this question. If you cannot get data on every observation in the population, you get a sample of the population, and given your sample is drawn randomly and the sample size is large enough, this will guide you accurately enough to understand the nature of the population. A statistic is just an approximation of the population parameter. In our case, the sample average is a good enough approximation of the population mean given you select the sample randomly.
In practical terms, if you ask your venture investor friends about their returns, even with the bold assumption of they tell the truth, you cannot get a good enough approximation of the average return for a venture capital fund. Why? You’ll have a hard time asking enough people (sampling error) and most importantly, your sample will not be random (sampling bias). In addition, power-law returns in venture pose extra challenges in going from sample averages to the population mean given the limitations of the famous law of large numbers theorem (more on this in the next part).
So, in light of all these, do we know the average return for a venture capital fund? Some people think we know the answer, but I don’t agree. Many rely on data providers like Prequin, Pitchbook, etc., firms that collect data on the basis of self-declaration, and by definition, their sample is not random. People self-declare data for a reason, and the most interesting venture returns I am aware of usually go undeclared.
The other data sources on venture capital returns are usually the firms that have asymmetric access to data in the opaque venture market due to their market positions like Angellist, Burgiss, Cambridge Associates, or fund-of-funds like Horsley Bridge (and Hummingbird!). Unfortunately, their data is not random either. There’s self-selection in funds that use particular service providers with respect to their needs. Also, fund-of-funds don’t operate randomly, so they reach out to a selected subset of funds and collect data on funds of certain relevance.
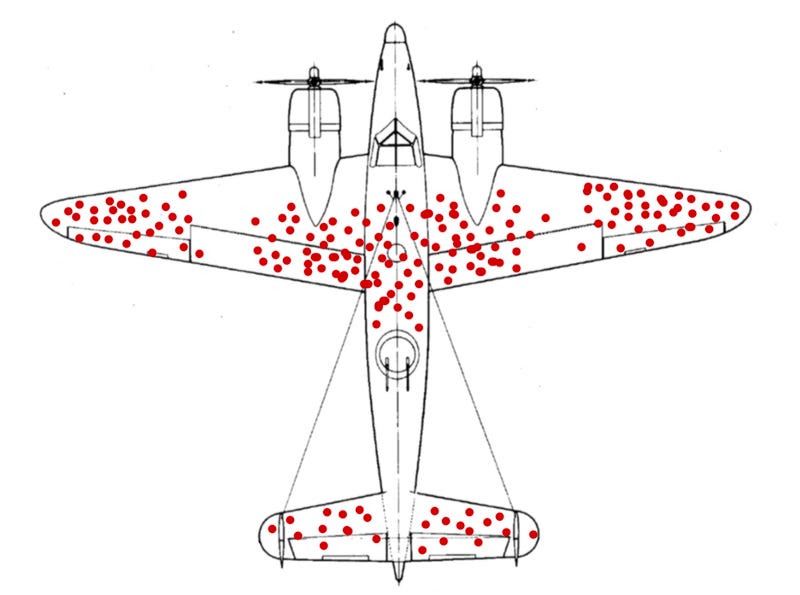
There’s the famous story of the mathematician Abraham Wald who worked in the US airforce to reinforce fighter planes during WWII. Looking at the returning planes, one would think reinforcing wings and fuselage was a good idea as these were the surfaces being hit. Wald’s idea was: “We only observe the ones that have returned, what about the ones being shut down and never returned? Shouldn’t they be the key object of observation?”
Similar survivorship bias is also observed in venture fund returns. Funds generating the most exceptional outcomes usually stop taking outside money, go stealth very quickly and their returns are rarely in any books, certainly not in your average private markets data provider. And the worst-performing funds fail to raise a successive fund. That’s not good news for the data quality in an industry that’s driven by outlier outcomes.
Lamplight probabilities, a term connoted by Bart Kosko, refers to the joke about the drunk who lost his keys somewhere in the dark and looks for them under the streetlamp because that’s where the light is. When it comes to statistics, venture capital people are no different. The data we have is far from representing the truth, it’s just convenient to use.
On average, I feel fine
There’s this story of the poor guy with one leg in an ice bucket and the other in boiling water, saying “On average, I feel fine.” It’s a good one to outline the limitations of averages. The averages are even more deceptive in venture capital, further complicating the simplest question of all.
Some variables in life are distributed normally, LeBron James entering a pub doesn’t shift the average height much. However, wealth isn’t distributed normally as in the story of Jeff Bezos entering a pub making everybody a millionaire. Financial returns of early-stage technology companies are similar to that as Amazon going into a portfolio early enough can also make everybody a millionaire.
Nassim Taleb coins such environments as Extremistan, where the results are driven by extreme events with low likelihood, but outsized impact. In Extremistan, the standard statistical toolkit proves to be useless for the most part, and the venture capital industry where only a handful of companies drive success is another good example of it.
Taleb also coins the term inverse problem, the fact that in real life we observe events without knowing or observing their statistical properties. Many different statistical distributions can correspond to the same set of realizations in real life. The fact that you haven’t seen a black swan yet can mean there are no black swans but it can also mean that black swans are one in a million. And, both of these statistical distributions extrapolate differently outside of the set of events from which they were derived. For the former, you won’t see any black swans indeed, for the latter, you are yet to see one.
The rarer the event the more theory you need and the worse the inverse problem. To estimate a rare event, you need a sample size that is larger and larger in inverse proportion to the occurrence of the event. If a unicorn company would be one out of every fifty companies, then you’d need data from 500 companies to make a reasonable guess on the frequency. When it’s one out of every thousand companies, you need data from 10,000 companies. In the dynamically changing venture market, increasing the sample size means tapping into different timeframes, countries, or different business models that usually fail to be a proper representation of the business at hand.
Conditional probabilities also don’t work in Extremistan. They work wonders for life expectancy and life insurance companies. You’d expect a developed country female to live for 79 years. If somebody is 79 y.o., you’d expect her to live additional 10 years, additional 4.7 years for 90 y.o., 2.5 years for 100 y.o., and a few minutes for 140 y.o. For extreme events, this doesn’t work. Conditional on a war killing millions of people, it may kill 10 million people on average. But, conditional on a war killing 500 million people, it may kill billions or more. It’s the same for startups. Conditional on a startup reaching a $10b valuation, you cannot assume a plateau around $10.5b, the upside could rather be $100s of billions in some cases. As Taleb says, in Extremistan, there’s no typical failure or typical success.
On the positive side, in venture capital, one faces positive uncertainty and convex payoffs. The true mean is more likely to be underestimated based on past realizations. In line with this, most investors note that most failures in venture capital are failures of imagination. That also explains how good venture investors are full of imagination and optimism that allows seeing the true potential of businesses and entrepreneurs. Apply this optimism to banking, the result would be a catastrophe as we have already seen many times. Extreme events don’t fall according to the past and we are fools to believe that the biggest company there is should be equal to the biggest one we have observed.
Dynamic causality
We face many challenges in answering the simplest question of all, and in making interpolations. When this is the case, it’s a very ambitious goal to build statistical models in order to make extrapolations.
It’s not trivial to assume that a causal relationship between time t and t+1 will apply to t+1 and t+2. It’s even bolder to assume causal relationships where feedback cycles are longer. An average venture capital fund matures in 10+ years, so you need at least a decade to analyze meaningful data and make extrapolations on future funds.
However, in a decade, the world doesn’t stay the same. Take the example of a fund that has been investing in US enterprise software during 2010-2012 and turned out to be very successful. Translating this to a fund that is investing in US enterprise software during 2020-2022 assumes many things including:
You invest at similar valuations to 2010.
You invest in similar entrepreneurs to 2010.
You invest in similar business models to 2010.
There is the same number of venture capital firms and a similar level of competition as there were in 2010.
The decision-makers in the venture capital firm are the same and as fit as they were in 2010.
The economic productivity gains left to be supplied by enterprise software companies are the same as it was in 2010.
Some of these assumptions might still be true, but some aren’t. We cannot just close our eyes and pretend the world is the same as in 2010. Statistical models are good at burying such assumptions in footnotes so we don’t have to close our eyes.
Markets are made of individual agents who adjust their behavior in response to new information. Even if one finds out patterns in data that would survive for decades, the mere fact that it is a signal results in decay in predictive power. Charles Goodhart wrote in 1975: “Any observed statistical regularity will tend to collapse once pressure is placed upon it for control purposes. When a measure becomes a target, it ceases to be a good measure.” Venture capital is a red queen race, where one finds many patterns just to watch them becoming ineffective over time. Dropping out of college to build a company took a particular character in 2000, now it’s another cool thing to do.
Findings and non-findings
The abundance of data, although with questionable quality, and cheap computing power makes it trivial to find regularities in datasets. Here’s how. In most statistical analyses, we determine a certain confidence level and 95% is the most commonly used one. Let’s assume 100 people in different parts of the world run the same statistical analysis to ‘understand the impact of being a white male on startup success’. With a 95% confidence level, it is expected that 5 of them will reach findings of statistical significance by pure chance, even if there’s no causality at all.
That’s okay if all 100 studies get reported so we get to read all. As you already have suspected at this point that it might not be the case, I can assure you that it isn’t the case. Human beings love sensation. They like findings and don’t like nonfindings.
In academia, that’s called publication bias. Academic journals aren't interested in publishing ‘failure to find results’ or ‘replications of existing results’, they want to publish new results. In today’s publish-or-perish academia, new researchers don’t devote time to replicating existing statistical studies. And, non-findings don’t get published or reported most of the time. If your statistical analysis fails to find a result, you run a new regression thanks to infinite computing power and plentitude of data until you eventually reach a statistically significant finding. And by pure luck, if you run enough analyses, you’ll have a finding. It’s worse in a rather opaque business setting where you don’t even have a peer review mechanism or rarely being held responsible for your mathematical rigor.
The standard statistical literature assumes that we form the hypothesis first, select the analysis method, collect the data and then run the statistical analysis. In a world where you can randomly run infinite numbers of different analyses on different datasets, that’s rarely the case. Most of the time the reality is about spending enough computing power and trying different methodologies and datasets until you find a result that you can publish. Then, you don’t tell anybody about the backstory.
Nullius in Verba
Nullius in Verba is the motto of the Royal Society of London, the world’s first scientific institution. It means “Take nobody’s word for it.” and refers to empiricism, the bedrock of science, which also makes sense to apply in businesses and investing. Leveraging data and statistics is a good way to apply the motto, but it’s equally good to be aware of naive empiricism where we apply empirical methods to settings they are unfit for.
And, it’s good to be aware that black-box thinking and extreme trust in statistical methods are equally risky as taking somebody’s word for it. At the end of the day, you are taking a data scientist’s or some statistician’s word for it if you are illiterate to challenge the mathematics going into the analysis.
Far from being critical of the use of statistics in investing, all of the above arguments show how statistical methods are prone to misuse and how large are the stakes for the ones who use them in the right way—and also show how one needs to think for herself when it comes to statistics. Data can be a way to uncover the hidden truth, but most of the time it’s a way to cover a story. Let’s be more skeptical of its use, yet optimistic about its potential.
The skepticism isn’t where the story ends, it’s where the story starts.






So, so good!